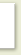Таким образом, простые числа – это как бы "кирпичики” для строительства всех натуральных чисел. Например, число N = 500 представимо в виде такого произведения:


Представление составного числа в указанном виде называют разложением числа на простые множители. Все, наверное, хорошо помнят эту процедуру, с которой познакомились ещё на уроках арифметики.

Деление производится до тех пор, пока слева не получается частное, равное 1; справа находятся простые множители, на которые разложено данное составное число. Однако не всегда так просто разложить заданное число на простые множители. Попробуйте-ка разложить на простые множители число N = 13593. Конечно, очевидно, что это число делится на 3, потому что сумма цифр числа делится на 3. Разделив число на 3, получаем число 4531. Это число не делится ни на 2, ни на 3, ни на 5, ни на 7. Итак, пока вы не дойдёте до первого простого числа, на которое полученное число делится, вы не продвинетесь ни на йоту в разложении этого числа на простые множители.

При разложении составного числа на простые множители используются признаки делимости. Признаки делимости на 2, 3 и 5 очень простые. Число делится: а) на 2 тогда и только тогда, когда его последняя цифра чётная; б) на 3 тогда и только тогда, когда сумма цифр этого числа делится на 3; в) на 5 тогда и только тогда, когда его последняя цифра 0 или 5. Признак делимости на 11: надо присвоить цифрам числа, начиная справа, попеременно знак "плюс” и знак "минус”, последняя цифра берётся со знаком "плюс”; затем сложить полученные значения. Исходное число делится на 11 тогда и только тогда, когда полученная сумма делится на 11. Пусть, например, надо определить, делится ли на 11 число 14399. Составляем сумму: 9 + (-9) + 3 + (-4) + 1 = 0. Полученная сумма делится на 11, следовательно, данное число тоже делится на 11. Так, можно сразу сказать, что любое число, составленное из чётного количества единиц (например: 1111, 11111111) делится на 11, а всякое число, составленное из нечётного количества единиц (например: 111, 1111111) не делится на 11. Точно так же можно определить, делится ли на 11, любое число, составленное другой цифрой, например: 3333333, 8888.

Признаков делимости на 7 существует несколько, но в [2] отмечается, что все они требуют не меньше затрат времени, чем обычное деление числа на 7. Это значит, что проще поделить число на 7 обычным образом, чем применять признак делимости. Подробнее о признаках делимости можно прочитать в [2].

Число 1 не относится к простым числам. "Математики предпочитают не считать 1 простым числом, поскольку в таком случае многие важные теоремы формулируются проще. Например, «основная теорема теории чисел» утверждает, что любое целое число допускает однозначное (с точностью до порядка множителей) разложение на простые множители. Так число 100 представимо в виде произведения четырёх простых множителей 2*2*5*5. Всякий другой набор (отличающийся хотя бы одним числом) простых множителей не даст в произведении числа 100. Если же считать единицу простым числом, то эта весьма важная теорема неверна: число 100 в этом случае представимо в виде произведения бесконечно многих различных наборов простых чисел, например, в виде 2*2*5*5*1*1”. [2]

Единственное чётное простое число 2. Все остальные простые числа нечётные, то есть любое простое число, отличное от 2, можно записать в виде: p = 2k + 1 (k >= 1).

Как уже сказано, множество простых чисел является подмножеством множества натуральных чисел. Как и множество натуральных чисел, множество простых чисел бесконечно. Это доказал Евклид. Приведу здесь доказательство этого утверждения, взятое в [3]. Положим, что ряд простых чисел ограничен и исчерпывается числами 2, 3, 5, …, p; в таком случае число N = (2*3*5* … *p) + 1, очевидно, не делится ни на 2, ни на 3, … ни на p, так как при делении на каждое из этих чисел мы получаем в остатке единицу. Поэтому должно иметь место одно из двух: либо это есть простое число, либо существуют простые числа, отличные от 2, 3, …, p. Но то и другое противоречит нашему предположению, и теорема, таким образом, доказана.
Для начала приведу ряд простых чисел в интервале (1, 500). Cделаю это в форме таблицы, чтобы лучше увидеть, как распределяются простые числа в  ряду натуральных чисел (рис. 1). Ячейки, содержащие простые числа, выделены оранжевым цветом.


Вот так причудливо располагаются простые числа в ряду натуральных чисел! Обратите внимание на простые числа, которые находятся рядом, например: 2 и 3; 5 и 7; 11 и 13; 17 и 19 и т. д. Такие пары простых чисел называются близнецами. До сих пор неизвестно, конечно или бесконечно число пар близнецов. Однако, ясно, что по мере возрастания чисел близнецы встречаются всё реже и реже.

Плотность распределения простых чисел среди натурального ряда различна, есть участки, где простые числа располагаются гуще. Вместе с тем, существуют целые оазисы, не содержащие ни одного простого числа. Справедливо следующее утверждение:


Предлагаю читателям доказать эту теорему.

Основная трудность в нахождении всех простых чисел состоит в том, что математикам не удаётся установить закон распределения простых чисел. Количество простых чисел, не превосходящих N, обозначается pi(N). Около 1800 г. два математика (А. Лежандр и К. Гаусс) независимо друг от друга высказали гипотезу, согласно которой

pi(N) примерно равно N/ln N

и что данное приближение тем лучше, чем больше N. Эта гипотеза впоследствии получила название теоремы об асимптотическом распределении простых чисел и была строго доказана в 1896 г. [2]

Например, количество простых чисел, не превосходящих 1000, оценивается числом 1000/ln1000, что примерно равно 145. Точное значение количества простых чисел, не превосходящих 1000, pi(1000) = 168.

Величина pi(N)/N называется средней плотностью простых чисел среди первых N натуральных чисел. Изучение таблиц простых чисел показывает, что с ростом N простые числа встречаются в среднем всё реже. Эйлер доказал, что lim (pi(N)/N) = 0 при N стремящемся к бесконечности. Отсюда, в частности, следует, что простые числа в среднем располагаются реже, чем члены какой угодно арифметической прогрессии. Можно доказать, что простые числа располагаются всё же гуще квадратов натуральных чисел.

В 1837 г. немецкий математик Л. Дирихле доказал, что в любой арифметической прогрессии, первый член и разность которой взаимно просты (определение взаимно простых чисел см. далее), есть бесконечно много простых чисел.

В 1852 г. П. Л. Чебышев доказал предположение французского математика Ж. Бертрана о том, что для любого натурального числа N между числами N и 2N всегда есть простое число. [5]

Примечание: портрет Леонарда Эйлера из [6].

Самый знаменитый квадратичный трёхчлен Л. Эйлера, производящий простые числа:
x^2 + x + 41

Первые 40 значений этого трёхчлена (при x = 0, 1, 2, …, 39) являются простыми числами.
Из 2398 первых значений, принимаемых этим трёхчленом, ровно половина - простые числа. Перебрав все значения знаменитого трёхчлена, не превышающие 10 000 000, Улам, Стейн и Уэллс обнаружили, что доля простых чисел среди них составляет 0, 475… . [2]

Составив программку вычисления значений данного трёхчлена Эйлера, я получила 200 первых значений (x принимает значения от 0 до 199). Вот они:
41 43  47  53  61  71  83  97  113  131  151  173  197  223  251  281  313  347  383  421  461  503  547  593  641  691  743  797  853  911  971  1033  1097  1163  1231  1301  1373  1447  1523  1601  1681  1763  1847  1933  2021  2111  2203  2297  2393  2491  2591  2693  2797  2903  3011  3121  3233  3347  3463  3581  3701  3823  3947  4073  4201  4331  4463  4597  4733  4871  5011  5153  5297  5443  5591  5741  5893  6047  6203  6361  6521  6683  6847  7013  7181  7351  7523  7697  7873  8051  8231  8413  8597  8783  8971  9161  9353  9547  9743  9941  10141  10343  10547  10753  10961  11171  11383  11597  11813  12031  12251  12473  12697  12923  13151  13381  13613  13847  14083  14321  14561  14803  15047  15293  15541  15791  16043  16297  16553  16811  17071  17333  17597  17863  18131  18401  18673  18947  19223  19501  19781  20063  20347  20633  20921  21211  21503  21797  22093  22391  22691  22993  23297  23603  23911  24221  24533  24847  25163  25481  25801  26123  26447  26773  27101  27431  27763  28097  28433  28771  29111  29453  29797  30143  30491  30841  31193  31547  31903  32261  32621  32983  33347  33713  34081  34451  34823  35197  35573  35951  36331  36713  37097  37483  37871  38261  38653  39047  39443  39841

Предлагаю читателям найти среди этих значений простые числа, не считая первых выделенных сорока.
Впоследствии подобные трёхчлены получили название "генераторы простых чисел” [7]. О спирали Улама см. в [2].

В этой спирали все 40 простых чисел, которые даёт рассматриваемый трёхчлен Эйлера при x = 0, 1, 2, …, 39, расположились на диагонали квадрата 40х40.
Аналогичный квадратичный трёхчлен, который тоже найден Эйлером: x^2 + x + 17. Этот трёхчлен при x, принимающем значения от 0 до 15, даёт только простые числа. На рис. 1б вы видите спираль Улама для этого трёхчлена.


Все 16 первых простых чисел, которые порождает данный трёхчлен, тоже расположились на диагонали квадрата. В квадрате выделены также остальные простые числа, находящиеся на этой спирали Улама. Интересно отметить, что те же самые 16 простых чисел этот трёхчлен даёт при x, принимающем значения от -1 до -16. Преобразовав рассматриваемый трёхчлен, можно получить такое выражение:

Новый трёхчлен порождает те же самые простые числа при y, принимающем значения от 1 до 16 (или при y = 0, -1, -2, …, -15). Точно так же можно записать и рассмотренный выше трёхчлен Эйлера:

Этот трёхчлен порождает те же самые 40 простых чисел при y = 1, 2, 3, …, 40 (или при y = 0, -1, -2, …, -39).
М. Гарднер в своей книге пишет: спираль Улама – забава, но её следует принимать всерьёз.

В [5] написано: легко доказать, что не существует многочлена от одной переменной, значения которого при всех целых значениях переменной есть простые числа. Вместе с тем, советский математик Ю. В. Матиясевич доказал, что существует многочлен от нескольких переменных, который принимает все простые значения по одному разу, причём все положительные его значения – простые числа.

И ещё одна формула для простых чисел была предложена П. Ферма. Он высказал предположение, что все числа вида 2^p + 1, где p = 2^k, простые. При k = 0, 1, 2, 3 , 4 получаются такие простые числа: 3, 5, 17, 257, 65537. Однако Эйлер опроверг это предположение, доказав, что при k = 5 число 2^p + 1 (p = 2^5) составное. В самом деле:

В [3] написано, что вопрос о том, при каких значениях k числа указанного вида являются простыми, остаётся и по сей день нерешённым. Вполне возможно, что в настоящее время уже есть ответ на этот вопрос или хотя бы приближение к ответу.

Примечание: портрет Пьера Ферма из [5].

Кстати, с простыми числами указанного вида связана задача  о том, какие правильные многоугольники можно построить с помощью циркуля и линейки. Гаусс установил, что для всех простых n, имеющих вид:

возможно деление окружности на равные части циркулем и линейкой; при других же простых значениях n такое деление невозможно.

Для случаев n = 3 и n = 5 деление окружности на n равных частей с помощью циркуля и линейки было хорошо известно ещё в древности. А вот построение правильного семнадцатиугольника посредством циркуля и линейки было обнаружено Гауссом впервые. [3]

Как уже было отмечено, современные компьютеры по составленным программам, заложенным в пакеты математических программ типа Maple, могут в считанные секунды проверить очень большие числа на простоту. Во времена Эйлера такая проверка даже для шести- и семизначных чисел требовала длительных вычислений. Эйлер однажды заявил, что число 1000009 простое, но потом обнаружил, что оно является произведением двух простых чисел: 293 и 3413. По тем временам это было крупное достижение, если к тому же учесть, что Эйлеру в это время было за 70 и он уже ослеп. Пьера Ферма в одном из писем спросили, простое ли число 100895598169. Он очень быстро ответил, что это число является произведением таких простых чисел: 898423 и 112303. В 1874 г. У. Стенли Джевонс вопрошал в своей книге "Основы науки”: "Может ли читатель сказать, произведение каких двух чисел равно 8616460799? Думаю, что вряд ли кто-нибудь, кроме меня самого, сумеет дать ответ на этот вопрос, ибо это два больших простых числа”. Конечно, Джевонс не мог знать, что современный компьютер найдёт оба эти числа быстрее, чем он мог бы их перемножить. [2]

Оказывается, натуральные числа раскладываются не только на произведение простых чисел, но и на сумму простых чисел. Это знаменитая проблема Х. Гольдбаха. Гольдбах высказал следующее предположение: а) всякое нечётное число, большее шести, есть сумма трёх простых чисел; б) всякое чётное число есть сумма двух простых чисел.

Например, 25 = 3 + 5 + 17, 26 = 7 + 19, 40 = 17 + 23.

В 1937 г. академик И. М. Виноградов с помощью разработанного им метода оценок тригонометрических сумм доказал, что каждое достаточно большое нечётное число действительно является суммой трёх простых чисел. [6]

Подробнее о других проблемах, связанных с простыми числами, смотрите в статье "Простые числа” в Википедии (ссылка в конце статьи). Как я поняла из этой статьи, проблема Гольдбаха не решена до сих пор.

Примечание: если число 1 не считать простым числом, то вторую часть гипотезы Гольдбаха следует сформулировать так: всякое чётное число большее 2 есть сумма двух простых чисел. Однако в [6], откуда я взяла приведённую формулировку этой гипотезы, написано так, как представлено выше. У меня возникает подозрение, что во времена Гольдбаха число 1 считалось простым числом. Тогда всё правильно, число 2 тоже представимо в виде суммы двух простых чисел: 1 + 1. В таком случае первая часть гипотезы автоматически следует из второй части, потому что любое нечётное число есть сумма чётного числа и единицы. Но тогда в первой части гипотезы непонятно ограничение "большее шести”.

В знаменитом магическом квадрате 3-го порядка из простых чисел, построенном Дьюдени, присутствует число 1. Есть это число и в известном магическом квадрате 12-го порядка из простых чисел Дж. Манси, построенном в 1913 г.

РЕШЕТО   ЭРАТОСФЕНА

Как же искать простые числа в ряду последовательных натуральных чисел? Древнейший алгоритм такого поиска был предложен 2000 лет назад астрономом и географом из Александрии Эратосфеном. Этот алгоритм получил название "решето Эратосфена”.

Опишу подробно алгоритм Эратосфена. Пусть нам надо найти все простые числа в диапазоне от 1 до N. Выпишем подряд все числа от 2 до N. Зачеркнём в этом списке каждое второе число из следующих за числом 2. Таким образом мы отсеем все числа кратные числу 2. Число 2 является первым простым числом.

Следующее не зачёркнутое число в списке после числа 2 – число 3. Это второе простое число. Повторим процедуру отсеивания, только теперь будем зачёркивать каждое третье число из следующих за числом 3. Так отсеем все числа кратные 3. Процедуру отсеивания следует повторять до тех пор, пока не доберёмся до простого числа, которое больше квадратного корня из N. Все числа, оставшиеся не зачёркнутыми в списке, будут простыми. Приведу иллюстрацию описанного метода для N = 50. Сначала покажу, как будет выглядеть список чисел после отсеивания чисел кратных 2:

2,  3,  /4/,  5,  /6/,  7,  /8/,  9,  /10/,  11,  /12/,  13,  /14/,  15,  /16/,  17,  /18/,  19,  /20/,  21,  /22/,  23,  /24/,  25,  /26/,  27,  /28/,  29,  /30/
31,  /32/,  33,  /34/,  35,  /36/,  37,  /38/,  39,  /40/,  41,  /42/,  43,  /44/,  45,  /46/,  47,  /48/,  49,  /50/

Примечание: зачёркнутые числа заключены в две наклонные черты / /.

Теперь покажу, как выглядит список после вычёркивания всех чисел кратных 3:
2,  3,  /4/,  5,  /6/,  7,  /8/,  /9/,  /10/,  11,  /12/,  13,  /14/,  /15/,  /16/,  17,  /18/,  19,  /20/,  /21/,  /22/,  23,  /24/,  25,  /26/,  /27/,  /28/,  29,  /30/
31,  /32/,  /33/,  /34/,  35,  /36/,  37,  /38/,  /39/,  /40/,  41,  /42/,  43,  /44/,  /45/,  /46/,  47,  /48/,  49,  /50/

Осталось два этапа: вычеркнуть все числа кратные 5 и кратные 7. Окончательно получим такой список простых чисел (простые числа выделены полужирным шрифтом):

2,  3,  /4/,  5,  /6/,  7,  /8/,  /9/,  /10/,  11,  /12/,  13,  /14/,  /15/,  /16/,  17,  /18/,  19,  /20/,  /21/,  /22/,  23,  /24/,  /25/,  /26/,  /27/,  /28/,  29,  /30/
31,  /32/,  /33/,  /34/,  /35/,  /36/,  37,  /38/,  /39/,  /40/,  41,  /42/,  43,  /44/,  /45/,  /46/,  47,  /48/,  /49/,  /50/

В этом примере процедура отсеивания (зачёркивания) завершилась на простом числе 7, то есть последний раз мы зачёркивали в этом списке каждое седьмое число, следующее за числом 7. Числа кратные 11 мы уже не будем зачёркивать (отсеивать), так как это число больше квадратного корня из 50.

Покажу ещё один оригинальный приём реализации решета Эратосфена из [2] (стр. 411 – 412). Здесь находятся все простые числа в интервале от 1 до 100. Все числа от 1 до 100 помещаются в прямоугольную таблицу (рис. 2).


Процедура отсеивания выполняется следующим образом. Вычеркнем все числа кратные 2, за исключением самой двойки, проведя вертикальные черты во втором, четвёртом и шестом столбцах. Вычеркнем все числа кратные 3 (сама тройка остаётся), проведя вертикальную черту в третьем столбце. Следующее за 3 не вычеркнутое число равно 5. Чтобы вычеркнуть числа кратные 5, проведём диагонали, идущие вниз и влево (число 5 остаётся). Оставшиеся в таблице числа кратные 7 вычеркнем, проведя диагонали с наклоном вправо и вниз. Наша работа по составлению списка простых чисел, не превосходящих числа 100, на этом заканчивается, поскольку следующее простое число 11 больше квадратного корня из 100. Если бы таблица была больше, то нам пришлось бы исключать числа кратные 11, проводя диагонали с более крутым наклоном. Все не зачёркнутые числа в таблице на рис. 2, кроме числа 1, являются простыми (они выделены красным цветом).

Во времена Эратосфена писали на восковых дощечках, а вместо того, чтобы числа зачёркивать, дощечку в нужном месте прокалывали. Отсюда и произошло название способа – "решето Эратосфена”: составные числа как бы "просеивались” в проколотые дырки, а простые числа оставались в "решете”.

Понятно, что алгоритм Эратосфена нетрудно реализовать. Существует множество программ, составленных разными авторами. Есть программа, например, в [4] (стр. 305). Можно посмотреть и реализацию алгоритма, выполненную в Википедии. А лучше всего составить свою программу.

Ещё одно интересное "решето” для нахождения простых чисел было предложено в 1934 году индийским математиком С. П. Сундарамом. Он придумал очень оригинальную таблицу, состоящую из бесконечного количества бесконечных арифметических прогрессий, причём каждый член первой прогрессии начинает новую прогрессию (с новой строки таблицы). Разностями прогрессий являются все нечётные числа, начиная с 3. На рис. 3 вы видите начало таблицы Сундарама.


Таблица бесконечно продолжается вправо и вниз. Разность арифметической прогрессии, записанной в первой строке таблицы, равна 3, разность арифметической прогрессии, записанной во второй строке таблицы, равна 5 и т. д. (все нечётные числа подряд являются разностями прогрессий).

Как же находить простые числа с помощью таблицы Сундарама? Оказывается, эта таблица обладает таким свойством: если некоторое число N содержится в таблице Сундарама, то число 2*N + 1 будет обязательно составным, а если число N не содержится в этой таблице, то число 2*N + 1 будет простым. Например, число 4 содержится в таблице, следовательно, число 2*4 + 1 = 9 составное; числа 5 нет в таблице, следовательно, число 2*5 + 1 = 11 простое. Доказательство этого свойства таблицы Сундарама вы можете найти в [1] (стр. 563 – 564).

Я реализовала метод Сундарама. Вот текст программы, написанный на языке QBASIC:

Программа для решета Сундарама:

5 PRINT "VVEDITE M"
7 INPUT M
8 IF INT(M / 2) <> M / 2 THEN 5
9 IF M < 4 THEN 5
10 PRINT "VVEDITE L"
11 INPUT L
12 FOR I = M + 1 TO L STEP 2
15 B = I: A = (B - 1) / 2
17 C = A - 1
20 FOR N = 1 TO C
25 K = (A - N) / (1 + 2 * N)
30 IF INT(K) = K THEN 40
35 NEXT N
36 W = W + 1: PRINT "#"; W
37 PRINT B
40 NEXT I
45 PRINT
50 END

Программа работает очень просто. Надо ввести в программу чётное натуральное число M >= 4 и любое натуральное число L > M. Программа выдаст все простые числа в диапазоне от M+1 до L. Недостаток программы: при M = 4 теряются два простых числа: 2 и 3. Но этот недостаток очень легко устранить, если вставить в программу блок простой печати указанных простых чисел в случае, когда M = 4. По этой программе я получила следующий ряд простых чисел в интервале от 5 до 1000 (M = 4, L = 1000):

5  7  11  13  17  19  23  29  31  37  41  43  47  53  59  61  67  71  73  79  83  89  97  101  103  107  109  113  127  131  137  139  149  151  157  163  167  173  179  181  191  193  197  199  211  223  227  229  233  239  241  251  257  263  269  271  277  281  283  293  307  311  313  317  331  337  347  349  353  359  367  373  379  383  389  397  401  409  419  421  431  433  439  443  449  457  461  463  467  479  487  491  499  503  509  521  523  541  547  557  563  569  571  577  587  593  599  601  607  613  617  619  631  641  643  647  653  659  661  673  677  683  691  701  709  719  727  733  739  743  751  757  761  769  773  787  797  809  811  821  823  827  829  839  853  857  859  863  877  881  883  887  907  911  919  929  937  941  947  953  967  971  977  983  991  997

Замечу, что при выполнении программы был открыт файл для вывода простых чисел. В приведённом варианте программы простые числа выводятся только на экран монитора. При этом перед каждым простым числом выводится его порядковый номер.

А это результат, выданный программой при M = 1000, L = 2000:

1009  1013  1019  1021  1031  1033  1039  1049  1051  1061  1063  1069  1087  1091  1093  1097  1103  1109  1117  1123  1129  1151  1153  1163  1171  1181  1187  1193  1201  1213  1217  1223  1229  1231  1237  1249  1259  1277  1279  1283  1289  1291  1297  1301  1303  1307  1319  1321  1327  1361  1367  1373  1381  1399  1409  1423  1427  1429  1433  1439  1447  1451  1453  1459  1471  1481  1483  1487  1489  1493  1499  1511  1523  1531  1543  1549  1553  1559  1567  1571  1579  1583  1597  1601  1607  1609  1613  1619  1621  1627  1637  1657  1663  1667  1669  1693  1697  1699  1709  1721  1723  1733  1741  1747  1753  1759  1777  1783  1787  1789  1801  1811  1823  1831  1847  1861  1867  1871  1873  1877  1879  1889  1901  1907  1913  1931  1933  1949  1951  1973  1979  1987  1993  1997  1999

На форуме dxdy.ru по моей просьбе приведённая программа переписана на двух других языках программирования: Pascal и Turbo C++ 3.0. Вы можете посмотреть эти программы по следующей ссылке.

В моей реализации решета Сундарама использовано следующее утверждение:


Теорема доказывается просто. Оставляю доказательство читателям.

Другую программу для решета Сундарама вы можете найти в Википедии в статье "Решето Сундарама”.

Отмечу, что в программе, приведённой в указанной статье Википедии, простые числа находятся только с начала ряда натуральных чисел до некоторого n. В этом неудобство программы в тех случаях, когда простые числа надо найти в некотором интервале, находящемся не в начале натурального ряда. Кроме того, моя реализация принципиально отличается от реализации, приведённой в Википедии. В моей программе меньше циклов и поэтому выполняется она быстрее.

Однако решето Сундарама в любом случае не работает для очень больших чисел за реальное время. Так, например, я смогла выполнить свою программу для интервала [10^7 + 1, 10^7 + 100) довольно быстро, а при M = 10^8, L = 10^8 + 100 программа надолго "задумалась”; я не стала ждать, когда она что-нибудь выдаст, и прервала её.

Приведу интересную задачу о простых числах, состоящих из единиц. Генри Э. Дьюдени ещё в 1907 году отметил, что  11 – единственное из известных в то время простых чисел, которое состоит из одних единиц. Понятно, что число, в записи которого участвует любая другая цифра, составное, например: 3333, 55555. Дьюдени доказал, что все числа, состоящие из 3, 4, 5, … , 18 единиц, составные.

Следует заметить, что справедлива следующая теорема:


Теорема доказывается очень просто.

Дьюдени заинтересовался такими "единичными” простыми числами. Один из его читателей доказал, что число, состоящее из 19 единиц, простое. Позднее было установлено, что число, записанное с помощью 23 единиц, также простое. В то время, когда я писала книгу, было известно, что числа, состоящие из 29, 31, 37, 41, 43, 53, 61 и 73 единиц, составные. Первым кандидатом на простое было число, составленное из 47 единиц. Я попробовала решить эту задачу, то есть установить, является ли число, состоящее из 47 единиц, простым. И сделать это пыталась как раз с помощью приведённой в теореме 2 формулы. Обозначим число, состоящее из 47 единиц, В. Чтобы ответить на вопрос, является число В простым или составным, надо установить, находится ли соответствующее ему число А в таблице Сундарама. Число А находится из уравнения:

Получаем, что число А = 55…5 (в записи числа А имеется 46 пятёрок).

Согласно теореме 2, если число А находится в таблице Сундарама, то оно должно быть представимо в виде:
где K и N – натуральные числа.

Следовательно, задача свелась к решению приведённого уравнения в натуральных числах. Удобнее представить это уравнение в таком виде:

Эта формула и положена в основу моей реализации решета Сундарама. Если данное уравнение не имеет решения в натуральных числах, то числа А нет в таблице Сундарама, а это означает, что соответствующее число В = 2 * А + 1 простое.

Однако для числа А, состоящего из 46 пятёрок, мне не удалось решить это уравнение (язык QBASIC не работает с такими большими числами). Поэтому эта задача тогда так и осталась у меня нерешённой.

Сейчас существует пакет математических программ Maple, который позволяет решать аналогичные задачи за одну секунду. На форуме, где я привела эту задачу, её решили сразу с помощью Maple. Оказалось, что число, составленное из 47 единиц, составное. Однако мне так и не ответили на вопрос, чему равны K и N, то есть в какой строке и с каким порядковым номером в этой строке находится в таблице Сундарама число А, состоящее из 46 пятёрок. А коль скоро число В, состоящее из 47 единиц, составное, число А, состоящее из 46 пятёрок, обязательно содержится в таблице Сундарама.

Приведу пример для небольшого числа А. Пусть А = 5555. В этом случае уравнение [1] имеет такое решение: N = 20, K = 135. Это значит, что в 20-ой строке таблицы Сундарама 135-ый член равен 5555, следовательно, число В = 2 * 5555 + 1 = 11111 составное.

Примечание: отмечу, что уравнение [1] в случае, когда число A содержится в таблице Сундарама, имеет не единственное решение. Рассмотрим пример для A = 22. Это число находится в таблице Сундарама в четырёх строках: первой, второй, четвёртой и седьмой.. Соответственно уравнение [1] имеет четыре решения:

1. N = 1, K = 7
2. N = 2, K = 4
3. N = 4, K = 2
4. N = 7, K = 1.

Только при A = 4 решение уравнения [1] будет единственным: N = 1, K = 1.

Для решения вопроса, является число B = 2*A + 1 простым или составным, достаточно найти одно решение уравнения [1] в натуральных числах.

С помощью приведённой выше программы для решета Сундарама можно проверить не очень большое число, является ли оно простым. Приведу два примера.

Пример 1. Требуется проверить число 10^5 + 1. Введём в программу M = 10^5, L = 10^5 + 1. Программы выполнит проверку только одного числа M + 1 = 10^5 + 1. Результат – данное число составное.

Пример 2. Требуется проверить число 10^6 + 121. Введём в программу M = 10^6 + 120, L = 10^6 + 121. Программы выполнит проверку числа M + 1 = 10^6 + 121. Результат выполнения программы – это число простое (программа выведет его на экран монитора).

Ещё один алгоритм нахождения простых чисел не связан ни с решетом Эратосфена, ни с решетом Сундарама. Здесь всё выполняется, что называется, "в лоб”: для каждого числа N проверяется, нет ли у него делителей в интервале от 2 до [v N]. Реализацию этого алгоритма тоже можно найти в [4] (стр. 306). Впрочем, алгоритм очень просто реализовать.


Решето Аткина – это современный оптимизированный вариант решета Эратосфена.

Я не разбиралась с этим решетом. Предоставляю данный метод читателям для самостоятельного изучения. В помощь даю ссылку на форум "Портал Естественных Наук”, где в теме "Алгоритм «решета Эратосфена»” подробно рассматривается вопрос о решете Аткина, приведён текст программы, как я поняла, полученный из текста в Википедии незначительными изменениями.

ЧИСЛА   МЕРСЕННА

Числа вида 2^p – 1, где p – простое число, называются числами Мерсенна, впервые заметившего, что среди таких чисел много простых. В течение почти 200 лет математики считали, что число Мерсенна 2^67 – 1 простое. Эрик Темриль Белл в своей книге "Математика – царица и служанка науки” рассказывает о заседании американского математического общества, состоявшемся в октябре 1903 г. в Нью-Йорке, на котором выступил с сообщением профессор Коул. "Коул, человек немногословный, подошёл к доске и, не говоря ни слова, начал возводить 2 в степень 67. Затем он вычел из полученного числа 1 и, по-прежнему не говоря ни слова, перешёл на чистую часть доски, где столбиком перемножил два числа: 193707721 и 761838257287. Оба результата совпали… Впервые в истории американского математического общества его члены бурными аплодисментами приветствовали докладчика. Коул, так и не проронив ни слова, сел на место. Никто не задал ему ни одного вопроса. Через несколько лет Белл спросил у Коула, сколько времени тот потратил, чтобы разложить число на множители. ”Все воскресенья в течение трёх лет”, - ответил Коул. [2]

Далее приведены девять первых чисел Мерсенна, среди которых выделены полужирным шрифтом простые числа:

3,   7,   31,  127,   2047,  8191,  131071,  524287,  8388607

Как видите, среди первых девяти чисел Мерсенна только два составные. В то время, когда Гарднер писал свою книгу "Математические досуги”, было известно такое максимальное простое число Мерсенна: 2^11213 – 1. Запись этого числа содержит около 3376 цифр. Это число обнаружил в 1963 г. с помощью ЭВМ Дональд Б. Джиллис. Это же число являлось и самым большим из известных простых чисел. [2]

В [5] уже приводится гораздо большее простое число Мерсенна:  2^132049 – 1. И опять же это число было самым большим из известных простых чисел.

В настоящее время составлены специальные программы для поиска чисел Мерсенна. Смотрите, например, тему "Взаимно простые числа” форума "Портал Естественных Наук”.

В статье "Простые числа” Википедии (ссылку см. в конце второй части статьи) сообщается, что самым большим простым числом по состоянию на сентябрь 2008 г. является число Мерсенна  2^43112609 – 1. Оно было найдено 23 августа 2008 г. на математическом факультете университета UCLA в рамках проекта по распределённому поиску чисел Мерсенна GIMPS. В десятичной записи этого числа содержится около 13 миллионов цифр. Это 46-ое число Мерсенна. Насколько  понимаю, 47-ое число Мерсенна ещё не найдено.

Примечание: 12 апреля 2009 г. открыто 47-е простое число Мерсенна 2^42643801-1. Оно же является самым большим простым числом по состоянию на сентябрь 2010 г.

Поскольку для чисел Мерсенна существует тест проверки на простоту, уже несколько лет именно эти числа держат рекорд самого большого простого числа.

ВЗАИМНО ПРОСТЫЕ ЧИСЛА

Два числа n и m называются взаимно простыми, если они не имеют общих делителей, кроме 1. Обычно это записывают так: (n, m) = 1.

Так, например, числа 10 и 33 взаимно просты. Чтобы определить, являются ли два числа взаимно простыми, надо разложить их на простые множители.

Если p – простое число и a не делится на p, то n = (a^p-1 – 1) всегда делится на p. Эта теорема носит название "малой теоремы Ферма”; она имеет очень большое значение для теории сравнений.

Эйлер ввёл функцию ph(m), которая называется функцией Эйлера. Эта функция определяет количество натуральных чисел меньших числа m и взаимно простых с ним. Так, ph(6) = 2, ph(10) = 4. Если m простое число, то все меньшие числа взаимно просты с m и ph(m) = m – 1. Например, ph(11) = 10.

Эйлер обобщил малую теорему Ферма и доказал, что если a и m взаимно простые числа, то (a^ph(m) – 1) делится на m. Это утверждение называется теоремой Эйлера о сравнениях. [6]

Продолжение статьи